Основное уравнение состояния

Выражения, связывающие значения любой из функций состояния со значениями координат состояния, есть однозначные уравнения состояния термодинамической системы: U = U(S, V, …), Т = T(S, V, …), р = p(S, V, …) и т.п.

Если для простой термомеханической системы из уравнения Т = T(S, V) выразить энтропию через температуру и объем S = S(T, V), то можем получить зависимость, связывающую между собой те параметры системы, которые могут быть измерены:

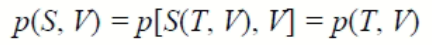
или

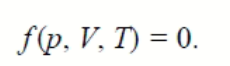
Состояние системы в таком случае определяется любой парой параметров, то есть любые два параметра из трех могут быть использованы в качестве независимых переменных.

При этих условиях свойства всех газов весьма схожи и их состояние описывается одинаковым для всех газов уравнением состояния идеального газа (уравнением Клапейрона‒Менделеева):

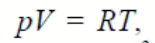
где V ‒ объем 1 кмоля вещества, м3/кмоль; R = 8,314 кДж/(кмоль·К) ‒ универсальная газовая постоянная, одинаковая для всех газов.

Уравнения состояния, предложенные для реальных газов, представляют собой, по существу, модификации уравнения состояния идеального газа, например уравнение Вандер-Ваальса:

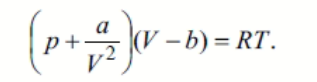
Или уравнение Камерлинг-Оннеса (1901). Оно выражает отклонение от уравнения состояния идеального газа в виде бесконечного степенного ряда по плотности:

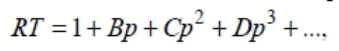
где В, С, D, … ‒ второй, третий, четвертый и т.д. коэффициенты, зависящие от температуры и природы газа и определяются экспериментально.

Поскольку изменение состояния сложной системы сопровождается изменением количества (массы) вещества в отдельных ее составляющих, то для полной характеристики состояния системы необходимо помимо термомеханических координат (S и V указывать также все химические координаты состояния.

Следовательно, уравнение состояния сложной системы связывает функцию состояния системы не только с двумя термомеханическими параметрами, определяющими состояние системы в процессе взаимодействия ее с окружающей средой, но и со значениями характеристики состава для всех составляющих сложной системы, определяющих состояние системы при фазовом или химическом взаимодействии между ее составляющими внутри системы, например:

n = vi – количество молей вещества в системе.